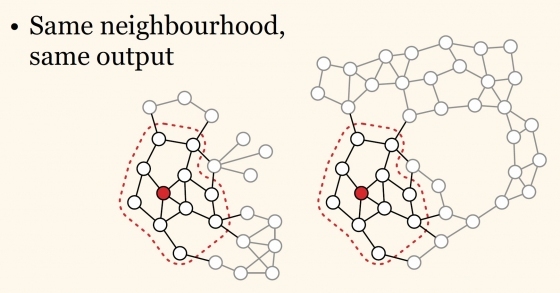
Soon, many network optimization problems will involve each node in the network making decisions to achieve a global objective.  Does the decision maker at a node need to know the structure of the whole network? Or is it sufficient to only know a small local neighborhood? The complexity of a network algorithm grows with the size of the local neighborhood.

Optimization problems are known to become difficult to solve as the density of the graph gets large.  Consider graph coloring.  It is much easier to identify a valid coloring for a sparse graph than a dense graph.  It is known that phase transitions occur in many random graph ensembles. 

Specifically, there is critical density threshold such that a graph is colorable with a fixed color budget with high probability below the density threshold, and not colorable with high probability above the density threshold.  In addition, the complexity of finding a valid coloring or proving that no coloring exists increases near the critical density threshold.

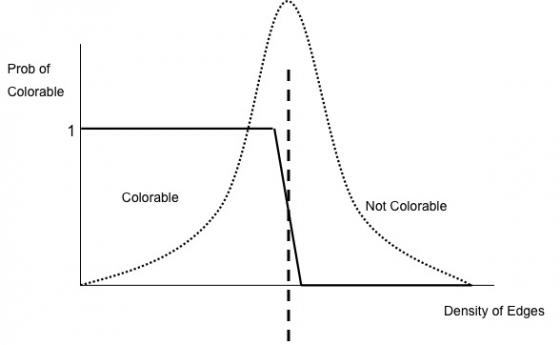
Colorability and complexity

Why are such problems difficult?  In the last decade, physicists have conjectured a detailed story, based on the theory of replica symmetry breaking of spin glasses, for explaining why these problems become hard to solve. In particular, they posit that the space of solutions is connected for low density graphs and becomes increasingly fractured as the density increases.

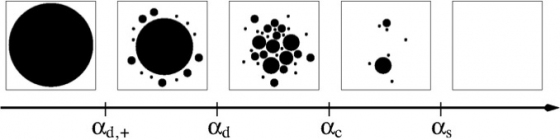
Clustering in the solution space (Krzakala PNAS 2007).

Our group is interested in determining what can be proven rigorously and what the implications are for efficient algorithm development.